python实现IQA图像质量评价

全称：Image Quality Assessment

百度百科 IQA：https://baike.baidu.com/item/IQA/19453034?fr=aladdin

主观评价

主观评价方法主要可分为两种：绝对评价和相对评价。

但是实现起来都有困难，这里先不考虑。

客观评价

全参考

基于图像像素统计基础

峰值信噪比（PSNR）：PSNR值越大，表明待评图像与参考图像之间的失真较小，图像质量较好
均方误差（MSE）：MSE的值越小，表明图像质量越好

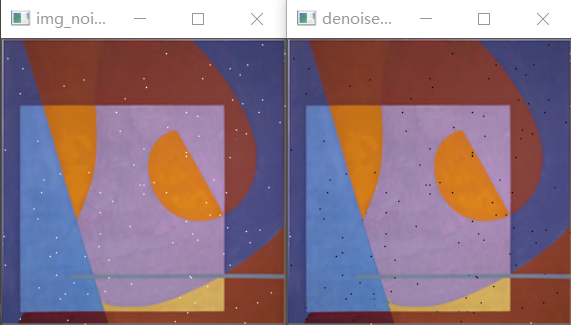
代码示例

import cv2 as cv
import numpy as np
import math


# 均方误差（MSE）：MSE的值越小，表明图像质量越好
def get_mse(img1, img2):
    return np.mean((img1 / 255. - img2 / 255.) ** 2)


# 峰值信噪比（PSNR）：PSNR值越大，表明待评图像与参考图像之间的失真较小，图像质量较好
# 基准为30dB，小于30为劣质
def get_psnr(img1, img2):
    mse = get_mse(img1, img2)
    if mse < 1.0e-10:
        return 100
    pixel_max = 1
    return 20 * math.log10(pixel_max / math.sqrt(mse))


if __name__ == '__main__':
    origin_img = cv.imread('img.png', 1)
    new_img = cv.imread('denoised_img_noise.png', 1)
    print('MSE:', get_mse(origin_img, new_img))
    print('PSNR:', get_psnr(origin_img, new_img))

结果

MSE: 0.0004777804926332579

PSNR: 33.20771586094474

从结果可以看出，上面测试使用的降噪后的图片质量还是可以的

基于信息论基础

基于信息论中信息熵基础，互信息被广泛用来评价图像质量。近些年，Sheikh和Bovik等人提出来了信息保真度准则（Information Fidelity Criterion,IFC）和视觉信息保真度（Visual Information Fidelity,VIF）两种算法。它们通过计算待评图像与参考图像之间的互信息来衡量待评图像的质量优劣。这两种方法具有一定的理论支撑，在信息保真度上拓展了图像与人眼之间的联系，但是这类方法对于图像的结构信息没有反应。

关于信息保真度准则（Information Fidelity Criterion,IFC）和视觉信息保真度（Visual Information Fidelity,VIF）这两种算法网上很难搜到合适的资料，即便能找到个别也都是matlab的，IFC方法到现在还没办法实现，下面是VIF方法。

代码示例

import numpy
import scipy.signal
import scipy.ndimage

__all__ = ['compare_vifp']


def compare_vifp(ref, dist):
    sigma_nsq = 2
    eps = 1e-10

    num = 0.0
    den = 0.0
    for scale in range(1, 5):

        N = 2 ** (4 - scale + 1) + 1
        sd = N / 5.0

        if scale > 1:
            ref = scipy.ndimage.gaussian_filter(ref, sd)
            dist = scipy.ndimage.gaussian_filter(dist, sd)
            ref = ref[::2, ::2]
            dist = dist[::2, ::2]

        mu1 = scipy.ndimage.gaussian_filter(ref, sd)
        mu2 = scipy.ndimage.gaussian_filter(dist, sd)
        mu1_sq = mu1 * mu1
        mu2_sq = mu2 * mu2
        mu1_mu2 = mu1 * mu2
        sigma1_sq = scipy.ndimage.gaussian_filter(ref * ref, sd) - mu1_sq
        sigma2_sq = scipy.ndimage.gaussian_filter(dist * dist, sd) - mu2_sq
        sigma12 = scipy.ndimage.gaussian_filter(ref * dist, sd) - mu1_mu2

        sigma1_sq[sigma1_sq < 0] = 0
        sigma2_sq[sigma2_sq < 0] = 0

        g = sigma12 / (sigma1_sq + eps)
        sv_sq = sigma2_sq - g * sigma12

        g[sigma1_sq < eps] = 0
        sv_sq[sigma1_sq < eps] = sigma2_sq[sigma1_sq < eps]
        sigma1_sq[sigma1_sq < eps] = 0

        g[sigma2_sq < eps] = 0
        sv_sq[sigma2_sq < eps] = 0

        sv_sq[g < 0] = sigma2_sq[g < 0]
        g[g < 0] = 0
        sv_sq[sv_sq <= eps] = eps

        num += numpy.sum(numpy.log10(1 + g * g * sigma1_sq / (sv_sq + sigma_nsq)))
        den += numpy.sum(numpy.log10(1 + sigma1_sq / sigma_nsq))

    vifp = num / den

    if numpy.isnan(vifp):
        return 1.0
    else:
        return vifp

结果

运用相同的测试图片，可以得到结果：

VIF: 0.9758460769325894

基于结构信息基础

SSIM：根据图像像素间的相关性构造出参考图像与待评图像之间的结构相似性，SSIM值越大，图像质量越好

PS：至此，找到更合理的代码方法

代码示例

import cv2 as cv
import numpy as np
import math
from skimage.metrics import mean_squared_error
from skimage.metrics import peak_signal_noise_ratio
from skimage.metrics import structural_similarity


# 均方误差（MSE）：MSE的值越小，表明图像质量越好
def get_mse(img1, img2):
    return np.mean((img1 / 255. - img2 / 255.) ** 2)


if __name__ == '__main__':
    origin_img = cv.imread('img.png', 1)
    new_img = cv.imread('denoised_img_noise.png', 1)

    # 均方误差（MSE）：MSE的值越小，表明图像质量越好
    mse = get_mse(origin_img, new_img)
    # 峰值信噪比（PSNR）：PSNR值越大，表明待评图像与参考图像之间的失真较小，图像质量较好
    # 基准为30dB，小于30为劣质
    psnr = peak_signal_noise_ratio(origin_img, new_img)
    # 结构相似度（Structural Similarity,SSIM），SSIM值越大，图像质量越好
    ssim = structural_similarity(origin_img, new_img, multichannel=True)

    print('MSE:', mse)
    print('PSNR:', psnr)
    print('SSIM:', ssim)

结果

MSE: 0.0004777804926332579

PSNR: 33.20771586094474

SSIM: 0.9570612590498769

存在的问题

我的代码中有这样的一行：from skimage.metrics import mean_squared_error

但是，在下方却没有用到mean_squared_error这一函数，这是因为在测试时，使用mean_squared_error函数得到的结果（30+）与自己写的get_mse函数的结果（0+）大相径庭，而网上的资源大多使用类似于get_mse的方法，而对mean_squared_error方法所提甚少，且从结果看，MSE算法的值也是应该越小越好，所以我暂时不使用mean_squared_error函数

部分参考

部分参考也成为半参考，它是以理想图像的部分特征信息作为参考，对待评图像进行比较分析，从而得到图像质量评价结果。由于所参考的信息是从图像中提取出来的特征，所以它必须要先提取待评图像和理想图像的部分特征信息，通过比较提取出的部分信息对待评图像进行质量评估。部分参考方法可分为基于原始图像特征方法、基于数字水印方法和基于Wavelet域统计模型的方法等。因为部分参考质量评价依赖于图像的部分特征，与图像整体相比而言，数据量下降了很多，目前应用比较集中在图像传输系统中。

这部分内容暂时也没有头绪，先放过