探索各种降噪算法的结果评价

A novel MR image denoising via LRMA and NLSS

作者

Chen, Z (Chen, Zhen) 1Fu, YL (Fu, Yuli) 1Xiang, YJ (Xiang, Youjun) 1Zhu, YH (Zhu, Yinhao) 1

SIGNAL PROCESSING

出版时间

AUG 2021

摘要

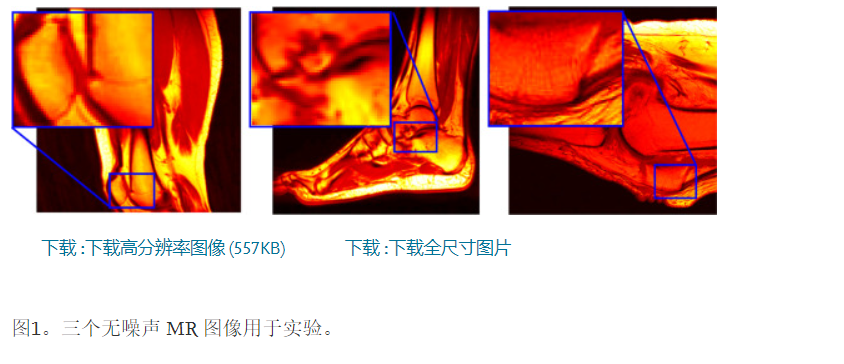
Nonlocal self-similarity has been proven to be a useful tool for image denoising. For MR image denois-ing, the method combining the nonlocal self-similarity with the low-rank approximation has been re-cently attracting considerable attentions, due to its favorable performance. Since the original low-rank approximation problem is difficult to be solved, the frequently used method is to use the nuclear norm minimization for the matrix low-rank approximation. However, the solution obtained by nuclear norm minimization generally deviates from the solution of the original problem. In this paper, an approach for MR image denoising is proposed by combining a novel nonlocal self-similarity scheme with a novel low-rank approximation scheme. In proposed approach, a similarity evaluation with respect to the noise is proposed in the patch matching stage. To approximate the original low-rank minimization problem, the propose approach minimizes trace-based operator at each step. Every minimization is solvable and used to approximate the original low-rank minimization. An algorithm is established for this approximation, as well. Experimental results show that the proposed approach has a superior performance, comparing with some of the low-rank approximation methods, in both the objective quality metrics and visual in-spections.

评估方式

参考

[1]

S. Li, H. Yin, L. FangGroup-sparse representation with dictionary learning for medical image denoising and fusionIEEE Trans. Biomed. Eng., 59 (12) (2012), pp. 3450-3459 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[2]

X. Mingliang, L. Pei, L. Mingyuan, F. Hao, Z. Hongling, Z. Bing, L. Yusong, Z. LiweiMedical image denoising by parallel non-local meansNeurocomputing, 195 (2016), pp. 117-122ArticleDownload PDFView Record in ScopusGoogle Scholar
[3]

H.V. Bhujle, S. ChaudhuriLaplacian based non-local means denoising of MR images with rician noiseMagn. Reson. Imaging, 31 (9) (2013), pp. 1599-1610ArticleDownload PDFView Record in ScopusGoogle Scholar
[4]

H. Liu, C. Yang, N. Pan, E. Song, R. GreenDenoising 3D MR images by the enhanced non-local means filter for rician noiseMagn. Reson. Imaging, 28 (10) (2010), pp. 1485-1496ArticleDownload PDFView Record in ScopusGoogle Scholar
[5]

Y. Fu, W. Dong3D Magnetic resonance image denoising using low-rank tensor approximationNeurocomputing, 195 (2016), pp. 30-39ArticleDownload PDFView Record in ScopusGoogle Scholar
[6]

K. Dabov, A. Foi, V. Katkovnik, K. EgiazarianImage denoising by sparse 3-d transform-domain collaborative filteringIEEE Trans. Image Process., 16 (8) (2007), pp. 2080-2095 Finding PDF…View Record in ScopusGoogle Scholar
[7]

J.F. Cai, Cand, E.J. S, Z. ShenA singular value thresholding algorithm for matrix completionSIAM J. Optim., 20 (4) (2008), pp. 1956-1982 Finding PDF…View Record in ScopusGoogle Scholar
[8]

Z. Chen, Z. Zhou, S. AdnanJoint low-rank prior and difference of gaussian filter for magnetic resonance image denoisingMedical & Biological Engineering & Computing, 59 (2021), pp. 607-620 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[9]

Z. Chen, Y. Fu, Y. Xiang, J. Xu, R. RongA novel low-rank model for MRI using the redundant wavelet tight frameNeurocomputing, 289 (2018), pp. 180-187ArticleDownload PDFView Record in ScopusGoogle Scholar
[10]

S. Gu, Q. Xie, D. Meng, W. Zuo, X. Feng, L. ZhangWeighted nuclear norm minimization and its applications to low level visionInt. J. Comput. Vis., 121 (2) (2017), pp. 183-208 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[11]

Y. Xia, Q. Gao, N. Cheng, Y. Lu, D. Zhang, Q. YeDenoising 3-D magnitude magnetic resonance images based on weighted nuclear norm minimizationBiomed. Signal Process. Control, 34 (2017), pp. 183-194ArticleDownload PDFView Record in ScopusGoogle Scholar
[12]

L. Jia, Z. Quan, Y. Wang, S. Yu, L. Yi, W. Na, Z. GuiDenoising for low-dose CT image by discriminative weighted nuclear norm minimizationIEEE Access, 6 (2018), pp. 46179-46193 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[13]

Y.-M. Huang, H.-Y. Yan, Y.-W. Wen, X. YangRank minimization with applications to image noise removalInf Sci (Ny), 429 (2018), pp. 147-163ArticleDownload PDFView Record in ScopusGoogle Scholar
[14]

L. Zhai, S. Fu, H. Lv, C. Zhang, F. WangWeighted schatten p-norm minimization for 3D magnetic resonance images denoisingBrain Res. Bull., 142 (2018), pp. 270-280ArticleDownload PDFView Record in ScopusGoogle Scholar
[15]

A.J. Miller, P.M. JosephThe use of power images to perform quantitative analysis on low SNR MR imagesMagn. Reson. Imaging, 11 (7) (1993), pp. 1051-1056ArticleDownload PDFView Record in ScopusGoogle Scholar
[16]

P. Coup, J.V. Manjn, E. Gedamu, D. Arnold, M. Robles, D.L. CollinsRobust rician noise estimation for MR imagesMed. Image Anal., 14 (4) (2010), pp. 483-493Google Scholar
[17]

S. Ajafernandez, C. Alberolalopez, C.F. WestinNoise and signal estimation in magnitude MRI and rician distributed images: a LMMSE approachIEEE Trans. Image Process., 17 (8) (2008), pp. 1383-1398 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[18]

J.V. Manjn, P. Coup, A. Buades, C.D. Louis, M. RoblesNew methods for MRI denoising based on sparseness and self-similarityMed. Image Anal., 16 (1) (2012), pp. 18-27Google Scholar
[19]

C. Pal, P. Das, A. Chakrabarti, R. GhoshRician noise removal in magnitude MRI images using efficient anisotropic diffusion filteringInt. J. Imaging Syst. Technol., 27 (3) (2017), pp. 248-264 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[20]

Geng, Chen, Yafeng, Wu, Dinggang, Shen, Pew-Thian, YapNoise reduction in diffusion MRI using non-local self-similar information in joint x-q space.Med. Image Anal., 53 (2019), pp. 79-94 Finding PDF…CrossRefGoogle Scholar
[21]

X. Jia, X. Feng, W. WangRank constrained nuclear norm minimization with application to image denoisingSignal Processing, 129 (2016), pp. 1-11ArticleDownload PDFCrossRefView Record in ScopusGoogle Scholar
[22]

E.J. Candes, Y. PlanMatrix completion with noiseProc. IEEE, 98 (6) (2009), pp. 925-936Google Scholar
[23]

E.J. Candes, T. TaoThe power of convex relaxation: near-optimal matrix completionIEEE Trans. Inf. Theory, 56 (5) (2010), pp. 2053-2080 Finding PDF…View Record in ScopusGoogle Scholar
[24]

C. Sun, D. RanRank-constrained optimization and its applicationsAutomatica, 82 (2017), pp. 128-136ArticleDownload PDFView Record in ScopusGoogle Scholar
[25]

R. Xiong, H. Liu, X. Zhang, J. Zhang, S. Ma, F. Wu, W. GaoImage denoising via bandwise adaptive modeling and regularization exploiting nonlocal similarityIEEE Trans. Image Process., 25 (12) (2016), pp. 5793-5805 Finding PDF…View Record in ScopusGoogle Scholar
[26]

L. Sendur, I.W. SelesnickBivariate shrinkage with local variance estimationSignal Processing Letters IEEE, 9 (12) (2002), pp. 438-441 Finding PDF…View Record in ScopusGoogle Scholar
[27]

M. LA trace inequality of john von neumannMonatshefte für Mathematik, 79 (1975), pp. 303-306Google Scholar
[28]

H. Mohimani, M. Babaie-Zadeh, C. JuttenA fast approach for overcomplete sparse decomposition based on smoothed ℓ0 normIEEE Trans. Signal Process., 57 (1) (2009), pp. 289-301 Finding PDF…View Record in ScopusGoogle Scholar
[29]

Q. Wang, X. Zhang, Y. Wu, L. Tang, Z. ZhaNon-convex weighted ℓp minimization based group sparse representation framework for image denoisingIEEE Signal Process. Lett., 24 (11) (2017), pp. 1686-1690 Finding PDF…View Record in ScopusGoogle Scholar
[30]

W. Dong, G. Shi, X. LiNonlocal image restoration with bilateral variance estimation: a low-rank approach.IEEE Trans. Image Process., 22 (2) (2013), pp. 700-711 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[31]

L. Ryan Wen, S. Lin, H. Wenhua, X. Jing, S.C.H. Yu, W. DefengGeneralized total variation-based MRI rician denoising model with spatially adaptive regularization parametersMagn. Reson. Imaging, 32 (6) (2014), pp. 702-720Google Scholar
[32]

Z. Wang, A.C. Bovik, H.R. Sheikh, E.P. SimoncelliImage quality assessment: from error visibility to structural similarityIEEE Trans Image Process, 13 (4) (2004), pp. 600-612 Finding PDF…CrossRefView Record in ScopusGoogle Scholar
[33]

L. Zhang, L. Zhang, X. Mou, D. ZhangFSIM: A feature similarity index for image quality assessmentIEEE Trans. Image Process., 20 (8) (2011), pp. 2378-2386 Finding PDF…View Record in ScopusGoogle Scholar

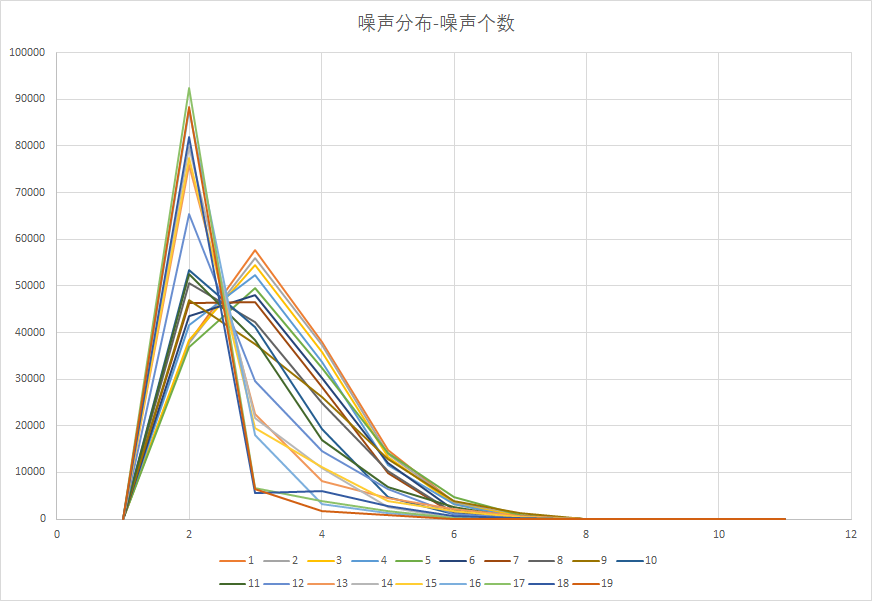
AUTOMATIC RANK ESTIMATION OF PARAFAC DECOMPOSITION AND APPLICATION TO MULTISPECT IMAGE WAVELET DENOISING

作者

Zidi, A (Zidi, Abir) 1Marot, J (Marot, Julien) 2Bourennane, S (Bourennane, Salah) 2Spinnler, K (Spinnler, Klaus) 1

摘要

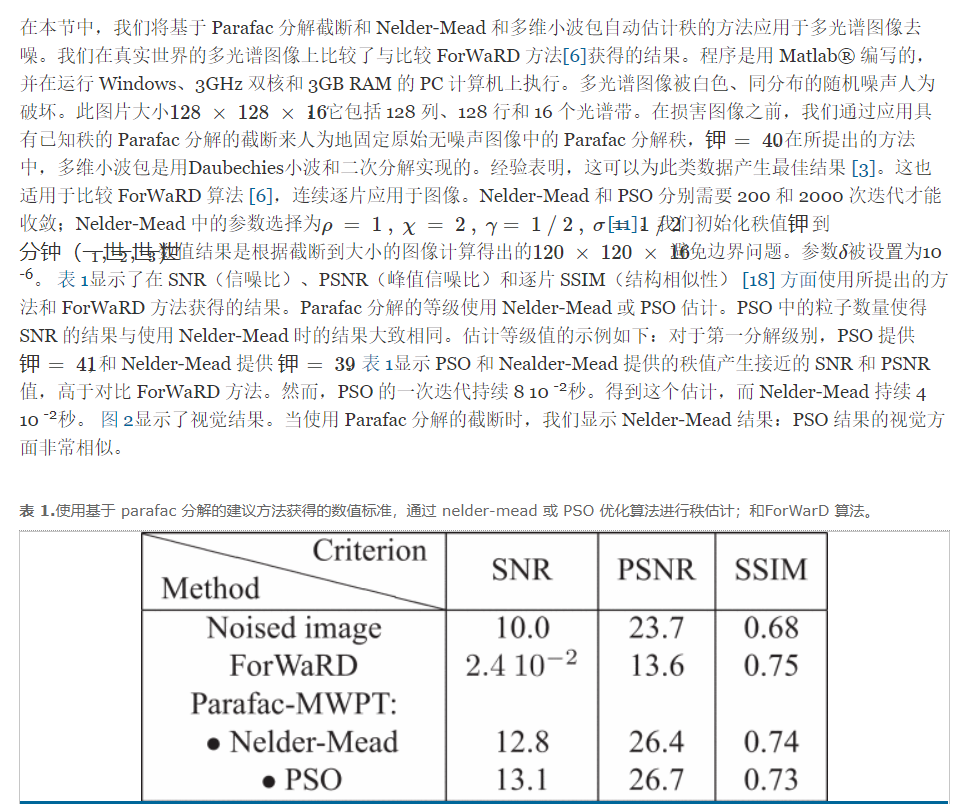
There are two main contributions in this paper. Firstly, we estimate the rank for the truncation of the Parafae decomposition in an optimal sense. For this, we propose a least squares criterion and justify the choice of the fast Nelder-Mead method to minimize this criterion. Secondly, we combine the truncation of the Parafac decomposition with multidimensional wavelet packet transform. A single rank value is estimated for each decomposition level, which simplifies the implementation. We exemplify the proposed method with an application to multispectral image denoising: we study the performance of the proposed method based on Parafac decomposition, compared to ForWaRD.

评估方式

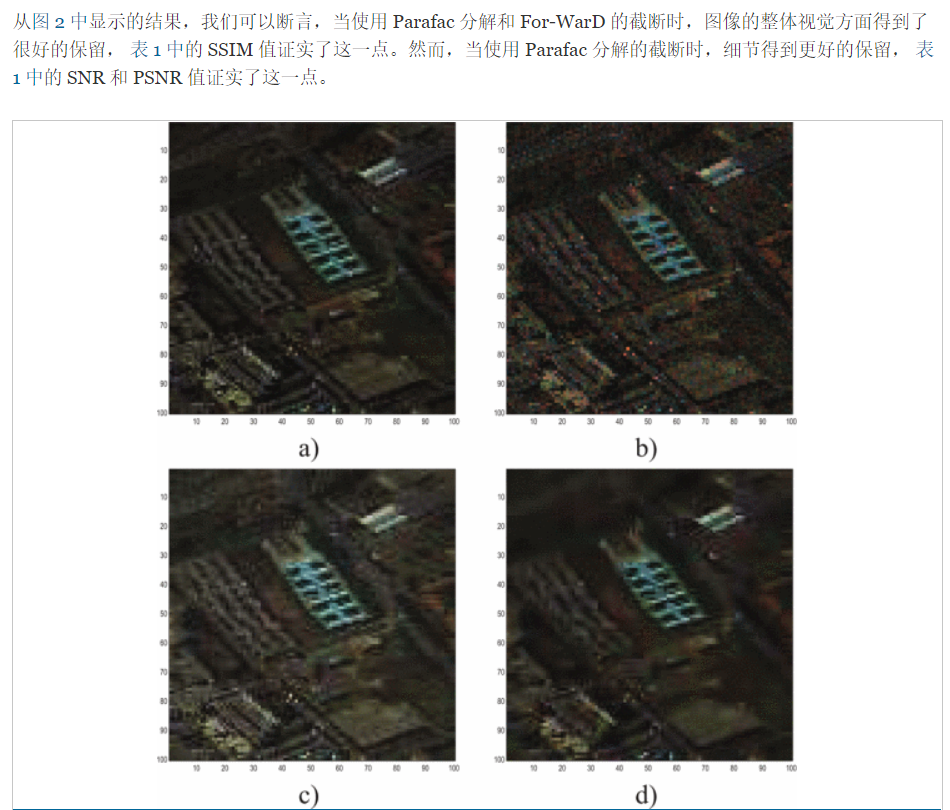
参考

**1.**D. Muti, S. Bourennane and J. Marot, “Lower-rank tensor approximation and multiway filtering”, SIAM Journal on Matrix Analysis and Applications, vol. 30, no. 3, pp. 1172-1204, 2008.

Show in Context CrossRef Google Scholar

**2.**M. Wei and D. Shen, “Minimum rank solutions to the matrix approximation problems in the spectral norm”, SIAM Journal on Matrix Analysis and Applications, vol. 33, no. 3, pp. 940-957, 2012.

Show in Context CrossRef Google Scholar

**3.**T. Lin and S. Bourennane, “Survey of hyperspectral image denoising methods based on tensor decompositions”, EURASIP Journal on Advances in Signal Processing, vol. 2013, no. 1, 2013.

Show in Context CrossRef Google Scholar

**4.**X. Liu, S. Bourennane and C. Fossati, “Reduction of signal-dependent noise from hyperspectral images for target detection”, IEEE trans. Geoscience and Remote Sensing, vol. 52, no. 9, pp. 5396-5411, Sept. 2014.

Show in Context Google Scholar

**5.**I. Daubechies, “Ten lectures on wavelets” in CBMS-NSF Lecture Notes, SIAM, no. 61, 1992.

Show in Context CrossRef Google Scholar

**6.**R. Neelamani, H. Choi and R. Baraniuk, “Forward: Fourier-wavelet regularized deconvolution for ill-conditioned systems”, IEEE Trans. on Signal Processing, vol. 52, no. 2, pp. 418-433, Feb 2004.

Show in Context View Article Full Text: PDF (630KB) Google Scholar

**7.**B. Tekin, U. Kamilov, E. Bostan and M. Unser, “Benefits of consistency in image denoising with steerable wavelets”, Acoustics Speech and Signal Processing (ICASSP) 2013 IEEE International Conference on, pp. 1355-1358, May 2013.

Show in Context Google Scholar

**8.**M. E. Timmerman and H. A. L. Kiers, “Three-mode principal components analysis: Choosing the numbers of components and sensitivity to local optima”, British Journal of Mathematical and Statistical Psychology, vol. 53, no. 1, pp. 1-16, 2000.

Show in Context CrossRef Google Scholar

**9.**E. Ceulemans and H. A. L. Kiers, “Selecting among three-mode principal component models of different types and complexities: A numerical convex hull based method”, British Journal of Mathematical and Statistical Psychology, vol. 59, no. 1, pp. 133-150, 2006.

Show in Context CrossRef Google Scholar

**10.**K. Liu, J. P. C. da Costa, H. C. So, L. Huang and J. Ye, “Detection of number of components in cande-comp/parafac models via minimum description length”, Digital Signal Processing, vol. 51, pp. 110-123, 2016.

Show in Context CrossRef Google Scholar

**11.**J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, “Convergence properties of the nelder-mead simplex method in low dimensions”, SIAM Journal of Optimization, vol. 9, no. 1, pp. 112-147, 1998.

Show in Context CrossRef Google Scholar

**12.**J. Kennedy and R. Eberhart, “Particle swarm optimization”, Proc. IEEE International Conference on Neural Networks, pp. 1942-1948, 1995.

Show in Context Google Scholar

**13.**L. Parra, C. Spence, P. Sajda, A. Ziehe and K. uller, “Unmixing hyperspectral data”, Advances in Neural Information Processing Systems, vol. 12, pp. 942-948, 2000.

Show in Context Google Scholar

**14.**T. G. Kolda and B. W. Bader, “Tensor decompositions and applications”, SIAM Review, vol. 51, no. 3, pp. 455-500, Sept. 2009.

Show in Context CrossRef Google Scholar

**15.**X. Liu, S. Bourennane and C. Fossati, “Nonwhite noise reduction in hyperspectral images”, IEEE trans. Geoscience and Remote Sensing Letters, vol. 9, no. 3, pp. 368-372, 2012.

Show in Context View Article Full Text: PDF (505KB) Google Scholar

**16.**D. Jones, C. Pertunen and B. Stuckman, “Lipschitzian optimization without the lipschitz constant”, Journal of Optimization theory and Application, vol. 79, no. 1, pp. 157-181, October 1993.

Show in Context CrossRef Google Scholar

**17.**F. Gao and L. Han, “Implementing the nelder-mead simplex algorithm withadaptive parameters”, Computational Optimization and Applications, vol. 51, no. 1, pp. 259-277, 2010.

Show in Context CrossRef Google Scholar

**18.**Z. Wang, A. Bovik, H. Sheikh and E. Simoncelli, “Image quality assessment: from error visibility to structural similarity”, Image Processing IEEE Transactions on, vol. 13, no. 4, pp. 600-612, 2004.

Show in Context View Article Full Text: PDF (1718KB) Google Scholar

Multidimensional Wiener filtering using fourth order statistics of hyperspectral images

作者

Letexier, D (Letexier, Damien) 1Bourennane, S (Bourennane, Salah) 1

摘要

In this paper we propose a new multidimensional filtering method based on fourth order cumulants to denoise of data tensor impaired by correlated gaussian noise. We overview the multidimensional Wiener filtering that overcomes the well known lower rank-(K-1,…, K-N) tensor approximation. But this method only exploits second order statistics. In some applications, it may be interesting to consider a correlated Gaussian noise. Then, we propose to introduce the fourth order statistics in the denoising algorithm. Indeed, the use of fourth order cumulants enables to remove the Gaussian components of an additive noise. Qualitative results of the improved multidimensional Wiener filtering are shown for the case of noise reduction in hyperspectral imagery.

评估方式

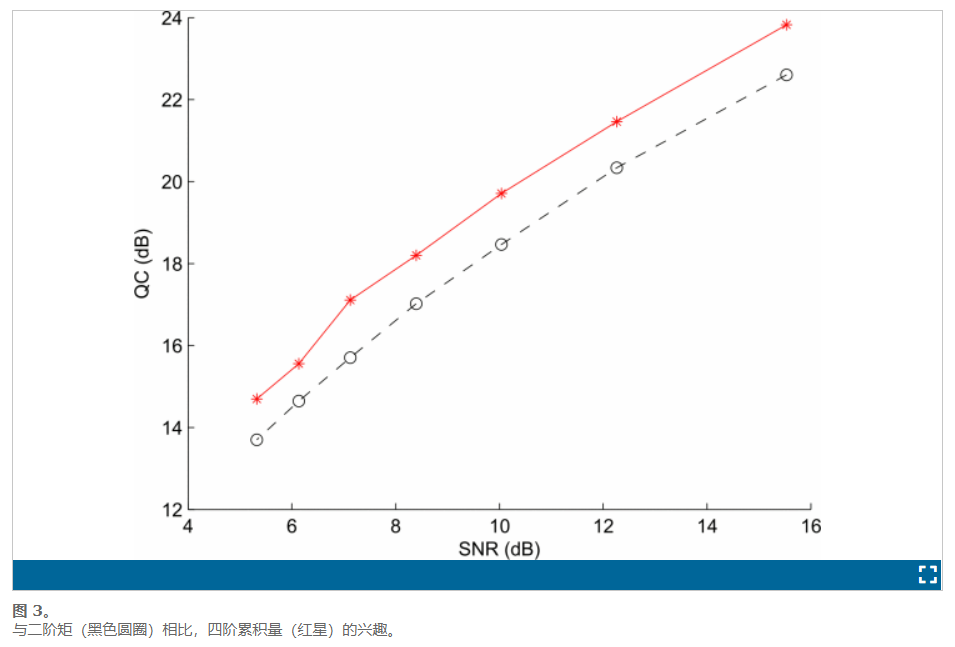
参考

**1.**L. De Lathauwer, B. De Moor, and J. Vandewalle, “A multilinear singular value decomposition,” SIAM Jour. on Matrix An. and Applic., vol. 21, pp. 1253-78, 2000.

Show in Context CrossRef Google Scholar

**2.**D. Muti and S. Bourennane, “Survey on tensor signal algebraic filtering,” Signal Processing, , no. 87, pp. 237-249, 2007.

Show in Context CrossRef Google Scholar

**3.**D. Letexier, S. Bourennane, and J. Blanc-Talon, “Nonorthogonal tensor matricization for hyperspectral image filtering,” IEEE Geoscience and Remote Sensing Letters, vol. 5, no. 1, 2008.

Show in Context View Article Full Text: PDF (560KB) Google Scholar

**4.**L. Tucker, “Some mathematical notes on three-mode factor analysis,” Psychometrika, vol. 31, pp. 279-311, 1966.

Show in Context CrossRef Google Scholar

**5.**L. Parra, C. Spence, P. Sajda, A. Ziehe, and K. uller, “Unmixing hyperspectral data,” Advances in Neural Information Processing Systems, vol. 12, pp. 942-948, 2000.

Show in Context Google Scholar

**6.**J.M. Mendel, “Tutorial on higher order statistics (spectra) in signal processing and system theory: theoretical results and some applications,” in Proc. of the IEEE, 1991, vol. 79, pp. 278-305.

Show in Context View Article Full Text: PDF (2709KB) Google Scholar

**7.**N. Yuen and B. Friedlander, “DOA in multipath: an approach using fourth order cumulant,” IEEE Trans. on Signal Process., vol. 45, no. 5, pp. 1253-63, 1997.

Show in Context View Article Full Text: PDF (405KB) Google Scholar

**8.**L. J. Rickard, R. W. Basedow, E. F. Zalewski, P. R. Silverglate, and M. Landers, “HYDICE: an airborne system for hyperspectral imaging,” in Proc. SPIE, Imaging Spect. of the Terrestrial Environment, G. Vane, Ed., 1993, vol. 1937, pp. 173-179.

Show in Context CrossRef Google Scholar

Wavelet Based Iterative Thresholding for Denoising of Remotely Sensed Optical and Synthetic Aperture Radar Images

作者

Ahmed, R (Ahmed, Rizwan) 1Maheshwari, N (Maheshwari, Niharika) 2Lalla, P (Lalla, Prithvi)

摘要

This article presents an overview of various denoising methods for optical and synthetic aperture radar (SAR) images. Currently, there are numerous algorithms and techniques to denoise images using adaptive filters in both the spatial as well as wavelet domain. However, in contrast, an algorithm which performs both soft and hard thresholding on a multi-level wavelet transformed image utilizing an adaptive threshold value has been designed and implemented. The threshold value varies for different wavelet regions from image to image and is selected for each region based on certain performance criteria such as Peak Signal to Noise Ratio (PSNR) and Mean Square Error (MSE). This algorithm has been used to denoise SAR images corrupted with multiplicative noise as well as optical images corrupted with White Gaussian additive noise. The results obtained have been compared with existing filters like median filter, Frost filter and Wiener filter. Additionally, we have compared the results of using different wavelet families including family of Daubechies and Biorthogonal filter banks.

评估方式

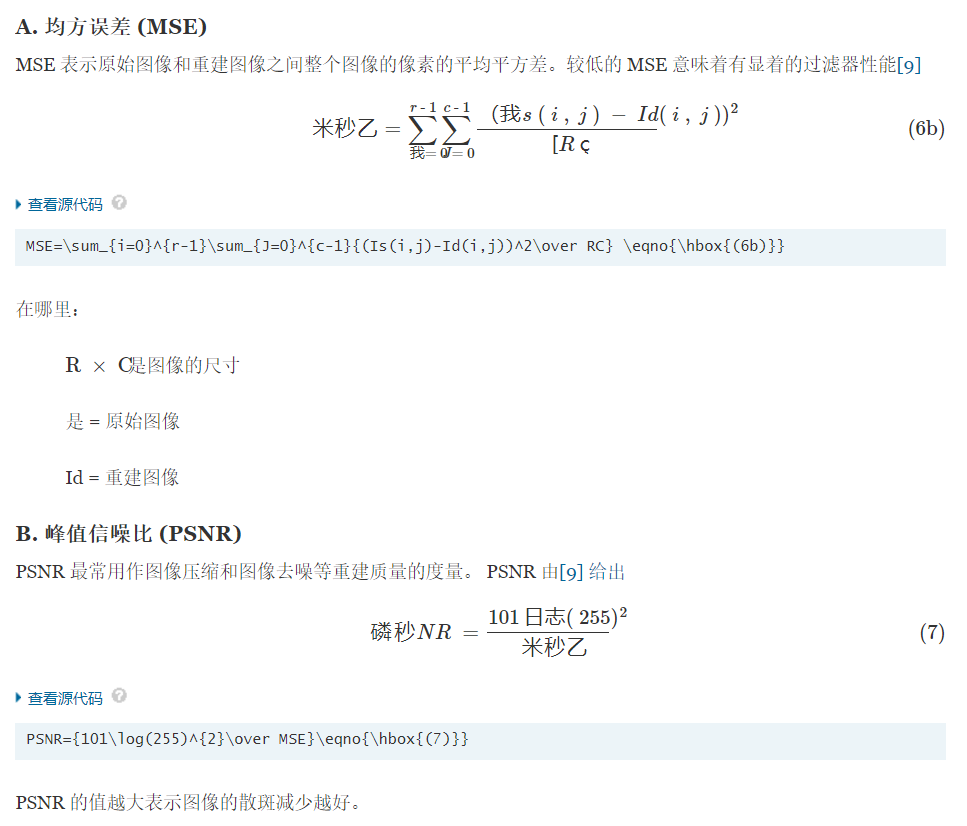
参考

**1.**Mallat S, “A wavelet tour of signal processing”, Academic press, 1999

Show in Context Google Scholar

**2.**Do D. L. Donoho, “Denoising by soft-thresholding,” IEEE Transactions on Infonnation Theory, vol. 41, no. 3, pp. 613-627,1995.

Show in Context View Article Full Text: PDF (1377KB) Google Scholar

**3.**Lee, “Refined filtering of image noise using local statistics,” CompuLGraph. Image Process., vol. 15, no. 4,1981

Show in Context CrossRef Google Scholar

**4.**V. S. Frost, J. A. Stiles, K. S. Shanmugan, and J. C. Holtzman, “A model for radar images and its application to adaptive digital filtering of multiplicative noise,” IEEE Trans. Pattern Anal. Machine Intell., vol. PAMI-4, Mar. 1980.

Show in Context Google Scholar

**5.**S. Mallat, “A theory for multi-resolution signal decomposition: The wavelet representation,” IEEE Trans. Pattern Anal. Machine Intell., vol. 11, pp. 674-693, July 1989.

Show in Context View Article Full Text: PDF (1797KB) Google Scholar

**6.**Gonzalez, Rafael C and Woods, Richard Eugene and Eddins, Steven L, “Digital image processing”, Pearson Education India, 2004.

Google Scholar

**7.**Chen, Guozhong and Liu, Xingzhao, “Wavelet-based despeckling SAR images using neighbouring wavelet coefficients”, Geoscience and Remote Sensing Symposium, 2005. IGARSS ‘OS. Proceedings. 2005 IEEE International, vol. 3, pp. 1764-1766,2005

View Article Full Text: PDF (288KB) Google Scholar

**8.**Makitalo, M and Foi, Alessandro and Fevralev, Dmitriy and Lukin, Vladimir, “Denoising of single-look SAR images based on variance stabilization and non local filters,” iEEE Proceedings on, Mathematical Methods in Electromagnetic Theory (MMET), pp. 1-4, 20 I 0

Google Scholar

**9.**Ali, Syed Musharaf and Javed, Muhammad Y ounus and Khattak, Naveed Sarfraz,” Wavelet-based despeckling of Synthetic Apelture Radar images using adaptive and mean filters”, International Journal of Computer Science & Engineering, vol. I, no. 2, 2007

Show in Context Google Scholar

**10.**A. Cohen and 1. Kovacevic, “Wavelets: The mathematical background,”Proc. IEEE, vol. 84, pp. 514-522, Apr. 1996.

View Article Full Text: PDF (880KB) Google Scholar

**11.**A. Graps, “An introduction to wavelets”, Computational Science & Engineering, IEEE, vol. 2, no. 2, pp. 50-61,1995.

Show in Context View Article Full Text: PDF (1095KB) Google Scholar

**12.**Chen, G and Zhu, W-P and Xie, W, “Wavelet-based image denoising using three scales of dependency”, IET, Image Processing, vol. 6, no. 6, pp. 756-760, 2012.

CrossRef Google Scholar

**13.**J. Daubechies. Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics,I 992.

Show in Context CrossRef Google Scholar

**14.**L. Gagnon and A. Jouan, “Speckle filtering of SAR images-A comparative study between complex-wavelet-based and standard filters,” Proc. SPIE, 1997.

CrossRef Google Scholar

New Method of Noise Removal in Images Using Curvelet Transform

作者

Kumar, S (Kumar, Sumit) 1Biswas, M (Biswas, Mantosh) 1

摘要

The term Curvelet transform in the field of Image Processing is quite well known from past few years. Its ability to detect curved features and smooth areas in an image marks its huge importance in the area of image denoising. However the ability to denoise image depends upon the selection and application of threshold after doing Curvelet based decomposition of an image. In this paper we are presenting our research methodology based on Curvelet transform image denoising. Our approach is based on the implementation of a modified window neighborhood processing that adapt itself based on the variance of neighboring pixels. We describe the problem we are considering for our research, present a brief overview of relative literature, describe the proposed methodology we have implemented and illustrate our future plan.

评估方式

参考

**1.**Starck Jean-Luc, Emmanuel J. Candes and David L. Donoho, “The curvelet transform for image denoising”, IEEE Transactions on image processing, vol. 11, no. 6, pp. 670-684, 2002.

Show in Context View Article Full Text: PDF (438KB) Google Scholar

**2.**N.N. Kachouie and P. Fieguth, “A combined Bayesshrink Wavelet-Ridgelet Technique for Image Denoising”, IEEE international Conference on Multimedia and Expo, pp. 1917-1920, 2006.

Show in Context Google Scholar

**3.**S.G. Chang, Yu Bin and M. Vitterli, “Adaptive Wavelet Thresholding for image Denoising and Compression”, IEEE Transactions on Image Processing, vol. 9, no. 9, pp. 1532-1546, 2000.

Show in Context Google Scholar

**4.**Jiang Tao, Zhao Xin, Ding Wenwen and Chen Junqing, “Improved Image Denoising method based on Curvelet Transform”, International Conference on Information and Automation, pp. 1086-1090, 2010.

Show in Context Google Scholar

**5.**Donglei Li, Zhemin Duan and Meng Jia, “New method based on curvelet transform for image denoising”, IEEE International Conference on Measuring Technology and Mechatronics Automation, vol. 2, pp. 760-763, 2010.

Show in Context Google Scholar

**6.**Qianzong Bao and Qingchun Li, “Translation invariant denoising using neighbouring curvelet coefficients”, 3rd International Workshop on Intelligent Systems and Applications, pp. 1-4, 2011.

Show in Context Google Scholar